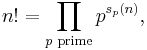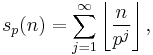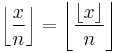De Polignac's formula

In number theory, de Polignac's formula, named after Alphonse de Polignac, gives the prime decomposition of the factorial n!, where n ≥ 1 is an integer. L. E. Dickson attributes the formula to Legendre.^[1]

The formula

Let n ≥ 1 be an integer. The prime decomposition of n! is given by

$n! = \prod_{p\text{ prime}} p^{s_p(n)},$

where

$s_p(n) = \sum_{j = 1}^\infty \left\lfloor\frac{n}{p^j}\right\rfloor,$

and the brackets represent the floor function. Note that the former product can equally well be taken only over primes less than or equal to n, and the latter sum can equally well be taken for j ranging from 1 to log_p(n).

Note that, for any real number x, and any integer n, we have:

$\left\lfloor\frac{x}{n}\right\rfloor = \left\lfloor\frac{\lfloor x \rfloor}{n}\right\rfloor$

which allows one to more easily compute the terms s_p(n).

Notes and references

^ Leonard Eugene Dickson, History of the Theory of Numbers, Volume 1, Carnegie Institution of Washington, 1919, page 263.